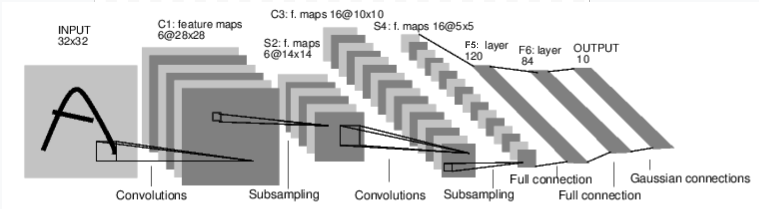
Stanford CNN
为什么普通神经网络不行
以计算机视觉领域为例,一张1000x1000的RGB照片,有1000x1000x3=3million个像素点,使用普通的神经网络,就有3M个输入特征,如果第二层有1000个神经元,二者之间的矩阵就是1000x3M=3billion个参数,太大了。
CNN base
假设要检测一张图像里物体的边缘。
single-channel filter
使用一个3x3的矩阵(称为filter,或者kernel,比如在pytorch里就是kernel),原图(假设为灰度图,6x6)卷积这个filter,会产生一个4x4的矩阵。
卷积是简单的对应位置数值相乘,求和,得出一个数。不是矩阵相乘。
如果这个filter选择的足够合适,就会在结果矩阵里产生明显的边界。
比如,假设数字越小越黑,越大越白,0基本是灰色:
\begin{bmatrix}
1&0&-1\\
1&0&-1\\
1&0&-1
\end{bmatrix}
是一个很好的检测vertical边界的矩阵。
某一块如果不是边缘,数值上应该变化不大,filter左边1,右边-1,乘完趋近于0。如果是边缘,数值变化较大,乘完不趋近于0(大于0或者小于0),所以乘出来的矩阵数字比较大的地方(产出的图片特别白或者特别黑的地方)就是原图的垂直边缘。
在卷积神经网络中,主要就是要学习出filter的参数,即这个3x3矩阵的9个参数。
同理,下面是一个水平边缘检测filter:
\begin{bmatrix}
1&1&1\\
0&0&0\\
-1&-1&-1
\end{bmatrix}
当然,也可以是其他的矩阵,不一定非得是这两个矩阵。具体用哪个,只要效果好就行。
padding
有两个问题:
- 每次图片和filter做一次卷积,尺寸都变小了一些;
- 原图的边缘像素,比如顶点位置只和filter乘了一次,但是中间位置的像素会和filter乘好几次,相当于在生成的结果中,原图每个像素所占比重不同了。
结果这两个问题的常用做法是padding:padding=1代表给原图加一圈像素。
- n:原图size;
- f:filter size;
- p:padding;
对于原图n=6,p=1之后,n变成了8,输出结果还是6x6。相当于图没变小。用公式表示,结果矩阵的size就是:(n+2p)-(f-1)
两种专业说法:
- valid convolution:no padding;
- same convolution:padding之后使输出尺寸等于输入,也就是(n+2p)-(f-1)=n,即
2p=f-1;
所以上述filter为3x3,p=1就能做到same padding。
计算机视觉里,使用的filter一般是奇数的,可能的原因有:
- 好填充,padding的时候一圈都填充就行了,而不是不对称填充;
- filter会有一个中心像素,所以好描述filter的位置;
遵守这个传统就行了。
strided 步长
横竖都应用步幅,大幅缩减生成矩阵的大小。
- s:strided size;
生成矩阵原来(strided=1时候)是(n+2p)-(f-1),strided之后要除以s,如果不是整数,向上取整即可。
cross-correlation vs. convolution
这里所说的convolution实际上不是数学上的convolution,而是cross-correlation,因为没有卷,只进行了积(对应位置元素相乘求和)。
卷的话就是把filter矩阵顺时针或者逆时针旋转180°
multi-channel filter
比如RGB图片有三个channel,filter也得是三个channel,才能做“体积上”的卷积操作。但是输出还是一个channel。即,输出矩阵的一个值,是filter和输入矩阵在“体积上”的乘积和。
filter和输入的channel必须相同。
所以,RGB的filter有三个channel,分别对应R,G,B层,去filter每一层。
multiple filters(multi-channel filter)
一个filter产生一层输出,多个filter叠加起来,就是多层输出。即 multiple multi-channel filters。
CNN layer
一般有三种layer:
- Conv: Convolution
- POOL: Pooling
- FC: Fully Connected
Conv
其实就是filter。
CNN:input x filter -> ReLU(非线性处理一下,激活函数) -> output
像极了普通神经网络:a2 = ReLU(W1*a1 + b1):
- filter = W1
- input = a1
一层CNN有多少个参数?假设有10个size=5,channel=3的filter,一个filter有5x5x3=75个参数,10个filter就是750个参数。(如果不考虑ReLU & bias的话)
一层CNN的参数跟input size有关吗?没关(当然,channel是要一致的),图片尺寸大点小点,不影响filter的尺寸。filter定义好size之后,参数个数是一定的,input大只会导致output大。
所以处理图片问题,CNN要比传统的神经网络好啊。传统神经网络处理的图片变大了,相当于特征变多了,W矩阵也要变大,参数就变多了。 那么我就有个问题了——假设以后计算能力无限扩大了,是不是不需要CNN了?
设计CNN,就是要设计一些超参数,比如多少个filter,padding多少,strided多少。
Pooling Layer
pool: to collect resource or sth.
比如Max pooling:
- input:4x4矩阵
- pool:2x2矩阵,strided=2。一般pooling layer的stide和size是一样的,这样就可以不重叠了;
- output:2x2矩阵
和卷积类似,但是简单很多。不是乘积求和,而是简单的比大小。
pooling layer的意义:减少representation(减小conv layer输出矩阵的大小),以此来提高网络的计算速度。
为什么可以这么做?假设是在检测图像中猫是否存在,现在无论如何都得扔掉一些像素,以使得网络计算速度加快。扔哪些?max pooling是在保留最大值,扔掉其他值,也就是说如果这一块区域没出现猫的特征相关数值,即使保留最大的值,也是很小的数字。同样是扔,这种扔法显然要比随机扔更有策略。
pooling layer vs. conv layer
- 操作方式相似,都是把一个input搞成output,流程也类似,只不过一个是卷积(乘积求和),另一个求max;
- pooling layer没有parameter!conv是求积再求和,既然求积,用哪个数和input相乘?得训练出来,这就是conv层的参数。pooling layer不一样,比如max pooling就是给input求个max,自己不需要有任何参数;
- max pooling一般不padding;
max pooling不是唯一的pooling,也有average pooling,但是现在都用max pooling,不怎么用average pooling了。
一般情况下,conv和pool合称一个layer,因为pooling layer没有参数。比如第一个layer,分别称为conv1和pool1。
FC layer
最后要把输出矩阵flatten一下,像传统神经网络一样,不停降元,最终输出为一个(logistic regression)或多个(1xn向量,分类问题)。
其实就是传统神经网络,叫做fully connection。
softmax
softmax函数:值输出转换为概率输出,用于多分类,相当于二分类里的sigmoid函数。比如分类结果有10中可能把一个1x10的向量(或者10x1,都行)的值输出转换为概率输出。
- https://deepai.org/machine-learning-glossary-and-terms/softmax-layer
CNN example
图画的和代码不太一致,维度有差别,仅参考结构即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
import torch
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
# 1 input image channel, 6 output channels, 3x3 square convolution
# kernel
self.conv1 = nn.Conv2d(1, 6, 3)
self.conv2 = nn.Conv2d(6, 16, 3)
# an affine operation: y = Wx + b
self.fc1 = nn.Linear(16 * 6 * 6, 120) # 6*6 from image dimension
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
# Max pooling over a (2, 2) window
x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
# If the size is a square you can only specify a single number
x = F.max_pool2d(F.relu(self.conv2(x)), 2)
x = x.view(-1, self.num_flat_features(x))
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
def num_flat_features(self, x):
size = x.size()[1:] # all dimensions except the batch dimension
num_features = 1
for s in size:
num_features *= s
return num_features
net = Net()
print(net)
input
32x32x1,灰度图片
conv1
Conv2d(1, 6, 3):
- 2d:图片,所以是2d;
- 1:input channel;
- 6:output channel;
- 3:filter size;
所以输入是32x32x1,输出是30x30x6。
pool1
max_pool2d(F.relu(self.conv1(x)), (2, 2)):
- 2d:图片,所以2d;
- (2, 2):kernel_size,也就是filter_size,方形的也可以传一个数值;
- stide默认是kernel_size,padding默认是0;
所以对conv1的输出做了一个ReLU,然后max pooling一下。
所以输出是15x15x6。
怎么知道channel是多少?看它的api,https://pytorch.org/docs/stable/generated/torch.nn.MaxPool2d.html:
1
2
3
Shape:
Input: (N, C, H_{in}, W_{in})
Output: (N, C, H_{out}, W_{out})
所以channel不变。
conv2
输入15x15x6,kernel_size=3,channel_out=16,所以输出是13x13x16
pool2
输入是13x13x16,输出是6x6x16。凑不成整数的扔了。
我记得是扔了。所以是6,而不是7
fc1
首先,flatten了一下,将conv和pool layer的输出搞成了一个一维向量。shape:1x(16x6x6)
关于torch.view改变tensor形状(其实就是reshape):
- https://stackoverflow.com/a/50793899/7676237
- https://pytorch.org/docs/stable/tensors.html#torch.Tensor.view
然后,使用普通神经网络的线性变换Linear(16x16x6, 120):
- 16x6x6=576: input,这是pool layer处理后的输出矩阵flatten之后的个数;
- 120:output
Linear的shape:
1
2
3
4
Shape:
Input: (N, *, H_{in}), where `*` means any number of additional dimensions and H_{in} = in_features
Output: (N, *, H_{out}), where all but the last dimension are the same shape as the input and H_{out} = out_features
和Andrew Ng不太相同的是,torch这里flatten之后是1xn的向量,Linear也是比较直白的input size -> output size。搞成1xn主要是因为Linear是特征向量乘以变换矩阵,而不是变换矩阵乘以特征向量。
输出是1x120
fc2
Linear(120, 84)
输入是1x120,输出是1x84
fc3
Linear(84, 10)
输入是1x84,输出是1x10
1x10对应十个输出结果。
至于softmax,这个网络没有定义。我看后续使用是拿着CNN得到的这个1x10的向量,使用
torch.max获取其最大值和index,直接把这个当做最终的预测结果。并不关心每一个的概率是多大。
形状概览
形状概览看到的只是这些layer的超参数:
1
2
3
4
5
6
7
Net(
(conv1): Conv2d(1, 6, kernel_size=(3, 3), stride=(1, 1))
(conv2): Conv2d(6, 16, kernel_size=(3, 3), stride=(1, 1))
(fc1): Linear(in_features=576, out_features=120, bias=True)
(fc2): Linear(in_features=120, out_features=84, bias=True)
(fc3): Linear(in_features=84, out_features=10, bias=True)
)
- 使用torch构建CNN时,不关心某个filter共计多少个参数。设置一下filter的超参数,只关心输入形状和输出形状。根据输出形状,设置下一个layer的超参数;
- 一般矩阵随着layer的层层递进,输出矩阵的size会减少,channel会变多;
why CNN?
传统神经网络其实就是fully connected neural network。
同样多的输入,想达到同样规模的输出,fc需要大量的参数矩阵,CNN却只需要几个filter,相比fc拥有少了好几个量级的参数。CNN怎么做到的?
parameter sharing input之间(output之间)共享参数
比如检测边界,一个3x3的filter,9个参数,可以被图片的不同位置共用。而检测边界只需要这样的9个参数就够了。
sparsity of connection 层与层之间的稀疏连接
CNN的下一层神经元和上一层的输入建立的是稀疏的连接,比如还是用3x3的filter的例子,一个output仅仅和3x3=9个input有关,和其他input无关。而fc则是全连接,一个output跟所有的input都有关联。所以参数多。
但实际上,比如一个图片,是一只猫,某些像素变了,它还是一只猫,如果是fc那种全连接,可能就得到不同的结果了。所以CNN和fc比,更robust,更适用于一些平移不变的特性。
ResNet - Residual Network 残差神经网络
网络层次越来越深,理论上会让结果越来越准确,但实际发现更难训练,而且效果还可能变差了。
ResNet:比如在训练第5层的时候,不仅使用第四层的输出,还是用第二层的输出,二者叠加。即:
1
a[5] = g((W*a[4] + b[4]) + a[2])
这样,因为W被纳入了cost function,所以W会比较小,即a5约等于直接g(a2),这意味着极限情况下,第三层和第四层被跳过去了。所以即使网络层次很深,多添加了几层(residual block),也不至于特别难训练,效果变差。最差a5效果和a2相同。而且,一旦这些residual block还学到了一些东西的话,效果会更好。
ResNet给人的感觉就是,想加深一下层次,让效果更好,但加深又不一定好,所以ResNet用shortcut短路掉这些新加的layer来保底,最差情况就是跳过被shortcut的layer,非最差情况下,又相当于不管怎样还是加了一些layer的。所以ResNet相当于加了零点几layer吧。
一个要注意的事情就是,a[2]和a[4]的维度应该相同。如果不同,就得给a[2]乘个系数矩阵,让他们维度相同。
1x1 convolution
如果input只有1个channel,使用1x1x1的convolution layer,就相当于给原来的input乘以一个plain number,没什么卵用。
如果input有多个channel,使用1x1xc_input的convolution相当于没有缩减input的size,但是控制filter的个数,可以改变output的channel。
其实相当于1x1的filter和input的一块做了一个fully connection。
和pooling layer相比,pooling layer主要是改变input的size(当然也能改变channel)。
如果pooling layer size=1,stride=1,就相当于是1x1的conv。这又印证了conv layer和pooling layer是非常相似的。
Inception Network
名字来源于盗梦空间Inception,In进入,cep拿。进入&拿,盗梦空间用了这个表面意思。(inception的实际意思是起始,开端)
Inception network只是借用了盗梦空间层层深入的意思,说明它是一层层深入的网络。
Inception network的思想就是:用1x1 filter还是3x3 filter?或者说用3x3的pooling layer而不是filtre?答案就是小孩子才做选择,我都要!把input用他们分别都处理一下,也就是说所有的layer都用到了,让他们有相同的output size(channel无所谓),然后再把这些output拼接起来,变成一个叠加channel的矩阵,作为下一层网络的output。
所以一般无论是conv layer还是pooling layer都做same convolution,让输出都和输入同size,这样所有的输出就同size,可以拼接了。
https://colah.github.io/posts/2014-07-Conv-Nets-Modular/